Conservation Laws |
||
|
|
||
In open tunnel and in regions alongside trains,
the equations of continuity and momentum are, for flow in an impervious
duct of constant cross-sectional area a and
perimeter  : |
||
 |
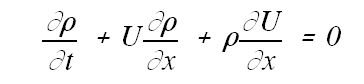(1) | |
| and |  |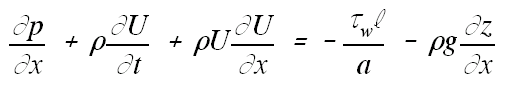
(2) |
respectively, where The air density and pressure are assumed to be related by the homentropic expression |
||
 |
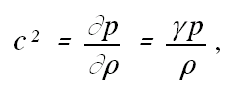(3) | |
where c denotes a local speed
of sound and Strictly, the use of Eq. 3 implies that entropy changes due to heat transfers and friction, etc exactly counterbalance one another. This is a somewhat arbitrary approximation, but it is useful because it greatly simplifies the analytical and numerical development and yet it has only a small influence on typical flows in railway tunnels during routine operation. The validity of the approach has been verified independently (eg: Woods,WA & Pope,CW, 1979). In this context, the parameter c should be interpreted exclusively as a pressure function. On no account should it be regarded as a measure of the temperature. Equation 3 can be used to eliminate |
||
 |
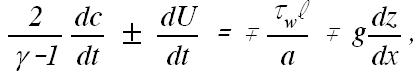(4) | |
in which dz/dx is assumed constant in time. These equations are valid in the Characteristic directions |
||
 |
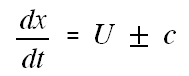(5) | |
respectively. Numerical integration |
||
|
|
||
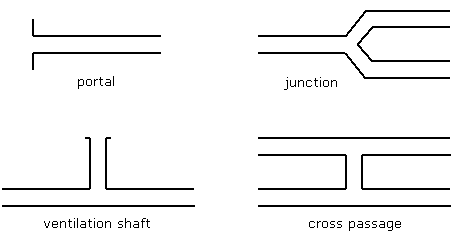
Equations 4 and 5 are integrated numerically at intersection points on a regular grid in time and space. The chosen time interval between successive calculations is approximately equal to the time required for a sound wave to travel from one grid point to the next. The procedure is outlined by Vardy (1976). Boundary conditions |
||
 |
||
| At tunnel junctions, the Bernoulli Sum B is assumed to be equal in all tunnels, subject to allowances for local losses. The continuity and Bernoulli equations are: | ||
 |
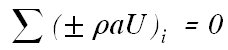(6) | |
 |
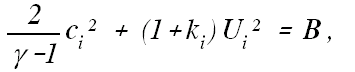(7) | |
| where ki is a local loss coefficient for flow into or out of the tunnel i. The conditions at the nose and tail of a train are analyzed in an identical manner relative to axes moving with the train. ReferencesVardy,AE (1976) 'On the use of the method of Characteristics for the solution of unsteady flows in networks', Proc 2nd int conf on Pressure Surges, BHRA Fluid Engrg, London UK, H2:15-30 Woods,WA & Pope,CW (1979) 'On the range of validity of simplified one dimensional theories for calculating unsteady flows in railway tunnels', Proc 3rd int symp on the Aerodynamics and Ventilation of Vehicle Tunnels, BHRA Fluid Engrg, Sheffield UK, D2:115-150 |
||
,
U and p are the
air density, mean velocity and pressure, 
is the wall shear stress and z is the elevation.
is
the ratio of the principal specific heat capacities of air.