ThermoTun - Governing Equations

Gas properties

The equation of state of a perfect gas may be written as

(1):  

in which p, r and T are the absolute pressure, the density and the absolute temperature.  The gas constant R is equal to Cp-Cv , where Cp and Cv are the specific heat capacities at constant pressure and constant density respectively.  For perfect gases, R, Cp and Cv are constants.  The speed of sound c satisfies

(2):   ,

where ( = Cp/Cv is the ratio of the specific heat capacities.

Continuity, momentum and energy

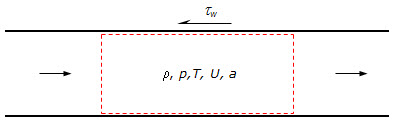
The equations of continuity, momentum and energy for unsteady flow in a horizontal duct of uniform area are

(3):  

(4):  

(5):   ,

in which  is the wall shear stress,  and  are the area and perimeter of the cross-section,  and  are rates of heat and work per unit mass and x and t are distance and time coordinates.  The parameters,  and  are flux correction coefficients that allow for non-uniform velocity distributions in the cross-section.  For simplicity, they are usually approximated to unity in ThermoTun.

Boundary conditions

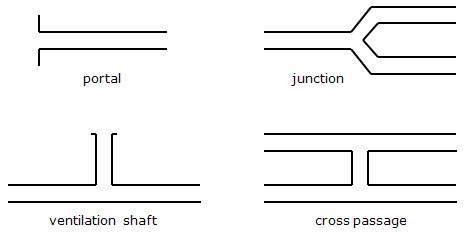
Equations 3-5 are applicable in regions of flow that may be regarded as continuous from a one-dimensional point of view – e.g. alongside a coach or between shafts in an open tunnel.  At discontinuities such as portals, junctions, fans and the ends of wagons, however, additional relationships are needed.  These ensure conservation of mass between adjacent regions of continuous flow and they prescribe:
  •         abrupt changes of stagnation pressure
  •         abrupt changes of stagnation temperature

In simple cases, the stagnation pressure might be prescribed to be equal at the ends of all tunnel regions connected to a boundary.  More generally, ThermoTun allows users to prescribe values of empirical loss coefficients that define differences of stagnation pressure across boundaries.  The stagnation temperature at a boundary/junction is determined by thorough mixing of all flows into the boundary.  The resulting mixture defines the stagnation temperature of flows out of the boundary.

Homentropic approximation (mode-5 only)

Versions of ThermoTun up to Ver5.2 used a simplified method of analysis in which the energy equation is replaced by two assumptions, namely:
  •         all flow processes take place isentropically
  •         all fluid particles have the same entropy
Together, these assumptions define a state of homentropic flow.  They greatly simplify the equations to be solved and they have been used by many analysts for flows where the influence of pressure changes dominates the influence of heat flows.  Versions of ThemoTun using these assumptions have given such good agreement with measurements at full-scale and model-scale that the approximation is still available (and widely used) in the latest versions of the software.

References

Vardy,AE (1976) 'On the use of the method of Characteristics for the solution of unsteady flows in networks', Proc 2nd int conf on Pressure Surges, BHRA Fluid Engrg, London UK, H2:15-30

Woods,WA & Pope,CW (1979) 'On the range of validity of simplified one dimensional theories for calculating unsteady flows in railway tunnels', Proc 3rd int symp on the Aerodynamics and Ventilation of Vehicle Tunnels, BHRA Fluid Engrg, Sheffield UK, D2:115-150